Maharashtra Board for Class 8, Maths Chapter 12

Class 8: Maths Chapter 12 solutions. Complete Class 8 Maths Chapter 12 Notes.

Contents

1 Maharashtra Board Solutions Class 8-Maths (Practice Set 12.2): Chapter 12- Equations in One Variable
2 Download PDF
3 Chapterwise Maharashtra Board Solutions Class 8 Maths :
4 FAQs
5 About Maharashtra State Board (MSBSHSE)

Maharashtra Board Solutions Class 8-Maths (Practice Set 12.2): Chapter 12- Equations in One Variable

Maharashtra Board 8th Maths Chapter 12, Class 8 Maths Chapter 12 solutions

Question 1.
Mother is 25 years older than her son. Find son’s age, if after 8 years ratio of son’s age to mother’s age will be \frac { 4 }{ 9 }49.
Solution:
Let the son’s present age be x years.
∴ Mother’s present age = (x + 25) years
After 8 years,
Son’s age = (x + 8) years
Mother’s age = (x + 25 + 8) = (x + 33) years
Since, the ratio of the son’s age to mother’s age after 8 years is \frac { 4 }{ 9 }49.
∴ \frac{x+8}{x+33}=\frac{4}{9}x+8x+33=49
∴ 9 (x + 8) = 4 (x + 33)
∴ 9x + 72 = 4x + 132
∴ 9x – 4x = 132 – 72
∴ 5x = 60
∴ x = \frac { 60 }{ 5 }605
∴ x = 12
∴ Son’s present age is 12 years.

Question 2.
The denominator of a fraction is greater than its numerator by 12. If the numerator is decreased by 2 and the denominator is increased by 7, the new fraction is equivalent to \frac { 1 }{ 2 }12 . Find the fraction.
Solution:
Let the numerator of the fraction be x.
The denominator of a fraction is greater than its numerator by 12.
∴ Denominator of the fraction = (x + 12)
∴ The required fraction = \frac { x }{ x+12 }xx+12
For the new fraction,
numerator is decreased by 2.
∴ The new numerator = (x – 2)
Also, denominator is increased by 7.
∴ The new denominator = (x + 12) + 7
= (x + 19)
Since, the new fraction is equivalent to \frac { 1 }{ 2 }12.
∴ \frac{x-2}{x+19}=\frac{1}{2}x−2x+19=12
∴ 2(x – 2) = 1(x + 19)
∴ 2x – 4 = x + 19
∴ 2x – x = 19 + 4
∴ x = 23
∴ The required fraction = \frac{x}{x+12}=\frac{23}{23+12}=\frac{23}{35}xx+12=2323+12=2335
∴ The required fraction is \frac { 23 }{ 35 }2335

Question 3.
The ratio of the weights of copper and zinc in brass is 13:7. Find the weight of zinc in a brass utensil weighing 700 gm.
Solution:
Let the weight of zinc in the brass utensil be x gm.
Since, the ratio of the weights of copper to zinc in brass is 13:7.

∴ Weight of copper in the brass utensil = \left(\frac{13}{7} x\right)(137x) gm
The weight of the brass utensil = 700 gm
∴ \frac { 13 }{ 7 }x+x=700137x+x=700
∴ \frac { 13 }{ 7 }x137x x × 7 + x × 7 = 700 × 7
∴ 13x + 7x = 4900
∴ 20x = 4900
∴ x=\frac { 4900 }{ 20 }x=490020
∴ x = 245
∴ The weight of zinc in the brass utensil is 245 gm.

Question 4.
Find three consecutive whole numbers whose sum is more than 45 but less than 54.
Solution:
Let the three consecutive whole numbers be (x – 1), x and (x + 1).
∴ Sum of the three numbers
= (x – 1) + x + (x + 1)
= 3x
Given that, the sum of the three numbers is greater than 45 and less than 54.
When the sum of the three numbers is 45,
3x = 45
∴ x = \frac { 45 }{ 3 }453
∴ x = 15
When the sum of the three numbers is 54,
∴ 3x = 54
∴ x = \frac { 54 }{ 3 }543
∴ x = 18
∴ the value of x is greater than 15 and less than 18.
∴ the value of x is either 16 or 17

Case I:
If the value of x is 16, then the three consecutive whole numbers are
(16 – 1), 16,(16 + 1)i.e., 15, 16, 17

Case II:
If the value of x is 17, then the three consecutive whole numbers are (17 – 1), 17, (17 + 1) i.e., 16, 17, 18.
∴ The three consecutive whole numbers are 15, 16, 17 or 16, 17, 18.

Question 5.
In a two-digit number, digit at the ten’s place is twice the digit at unit’s place. If the number obtained by interchanging the digits is added to the original number, the sum is 66. Find the number.
Solution:
Let the digit at unit’s place be x.
The digit at the ten’s place is twice the digit at unit’s place.
∴ The digit at ten’s place = 2x

	Digit in units place	Digit in tens place	Number
Original Number	x	2x	(2x × 10) + x = 20x + x = 21x
New Number	2x	x	(x × 10) + 2x = 10x + 2x = 12x

Since, the sum of the original number and the new number is 66.
∴ 21x + 12x = 66
∴ 33x = 66
∴ x = \frac { 66 }{ 33 }6633
∴ x = 2
∴ Original number = 21x = 21 × 2 = 42
∴ the original number is 42.

Question 6.
Some tickets of Rs 200 and some of Rs 100, of a drama in a theatre were sold. The number of tickets of Rs 200 sold was 20 more than the number of tickets of Rs 100. The total amount received by the theatre by sale of tickets was Rs 37000. Find the number of Rs 100 tickets sold.
Solution:
Let the number of tickets sold of Rs 100 be x.
The number of tickets of Rs 200 sold was 20 more than the number of tickets of Rs 100.
∴ Number of tickets sold of Rs 200 = (x + 20)
∴ Total amount received by the theatre through the sale of tickets = 100 × x + 200 × (x + 20)
= 100x + 200x + 4000
= 300x + 4000
Since, the total amount received by the theatre through the sale of tickets = Rs 37000
∴ 300x + 4000 = 37000
∴ 300x = 37000 – 4000
∴ 300x = 33000
∴ x=\frac { 33000 }{ 300 }x=33000300
∴ x = 110
∴ 110 tickets of Rs 100 were sold.

Question 7.
Of the three consecutive natural numbers, five times the smallest number is 9 more than four times the greatest number, find the numbers.
Solution:
Let the three consecutive natural numbers be (x – 1), x and (x + 1).
Here, the smallest number is (x – 1) and the greatest number is (x + 1).
Since, five times the smallest number is 9 more than four times the greatest number.
∴ 5 × (x – 1) = [4 × (x + 1)] + 9
∴ 5x – 5 = 4x + 4 + 9
∴ 5x – 5 = 4x + 13
∴ 5x – 4x = 13 + 5
∴ x = 18 .
∴ the three numbers are (18 – 1), 18, (18 + 1)
i. e., 17, 18, 19
∴ The three consecutive natural numbers are 17,18 and 19.

Question 8.
Raju sold a bicycle to Amit at 8% profit. Amit repaired it spending Rs 54. Then he sold the bicycle to Nikhil for Rs 1134 with no loss and no profit. Find the cost price of the bicycle for which Raju purchased it.
Solution:
Let the cost price at which Raju purchased the bicycle be Rs x.
Since, Raju sold the bicycle at 8% profit to Amit.
∴ Selling price of bicycle for Raju = x + 8% of x

Since, Amit spent Rs 54 on repairing the bicycle and then sold it to Nikhil for Rs 1134, at no loss and no profit.
∴ Selling price of bicycle + repairing cost = Rs 1134

∴ The cost price of the bicycle at which Raju purchased it is Rs 1000.

Question 9.
A cricket player scored 180 runs in the first match and 257 runs in the second match. Find the number of runs he should score in the third match so that the average of runs in the three matches be 230.
Solution:
Let the number of runs required by the cricket player to score in the third match be x.
Number of runs scored by the player in first match = 180
Number of runs scored in second match = 257
∴ Total runs scored by the player = 180 + 257 + x = 437 + x
Average of runs in the three matches = \frac { 437+x }{ 3 }437+x3
Since, the average of runs should be 230.
\frac { 437+x }{ 3 }=230437+x3=230
∴ 437 + x = 230 × 3
∴ 437 + x = 690
∴ x = 690 – 437
∴ x = 253
∴ The cricket player should score 253 runs in the third match.

Question 10.
Sudhir’s present age is 5 more than three times the age of Viru. Anil’s age is half the age of Sudhir. If the ratio of the sum of Sudhir’s and Viru’s age to three times Anil’s age is 5:6, then find Viru’s age.
Solution:
Let Viru’s present age be x years.
Sudhir’s present age is 5 more than three times the age of Viru.
∴ Sudhir’s present age = (3x + 5) years
Anil’s age is half the age of Sudhir.
∴ Anil’s present age = \left(\frac{3 x+5}{2}\right)(3x+52) years
Since, the ratio of the sum of Sudhir’s and Viru’s age to three times Anil’s age is 5:6.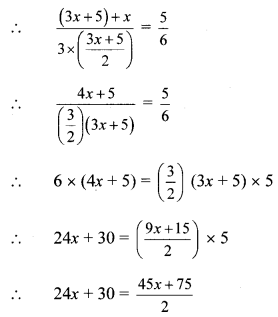

∴ 2 × (24x + 30) = 45x + 75
∴ 48x + 60 = 45x + 75
∴ 48x – 45x = 75 – 60
∴ 3x = 15
∴ x = \frac { 15 }{ 3 }153
∴ x = 5
∴ Viru’s present age is 5 years.

Intext Questions and Activities

Question 1.
Write correct numbers in the boxes given. (Textbook pg. no. 78)
length is 3 times the breadth

Perimeter of the rectangle = 40
2(__x + __x) = 40
2 × __ x = 40
__ x = 40
x = __
∴ Breadth of rectangle = __ cm and Length of rectangle = __ cm
Solution:
length is 3 times the breadth

Perimeter of the rectangle = 40
∴ 2(3x + 1x) = 40
∴ 2 × 4x = 40
∴ 8x = 40
∴ x = 5
∴ Breadth of rectangle = 5 cm and Length of rectangle = 15 cm

Download PDF

Maharashtra Board Solutions Class 8-Maths (Practice Set 12.2): Chapter 12- Equations in One Variable

Download PDF: Maharashtra Board Solutions Class 8-Maths (Practice Set 12.2): Chapter 12- Equations in One Variable PDF

Chapterwise Maharashtra Board Solutions Class 8 Maths :

FAQs

Where do I get the Maharashtra State Board Books PDF For free download?

You can download the Maharashtra State Board Books from the eBalbharti official website, i.e. cart.ebalbharati.in or from this article.

How to Download Maharashtra State Board Books?

Students can get the Maharashtra Books for primary, secondary, and senior secondary classes from here. You can view or download the Maharashtra State Board Books from this page or from the official website for free of cost. Students can follow the detailed steps below to visit the official website and download the e-books for all subjects or a specific subject in different mediums.
Step 1: Visit the official website ebalbharati.in
Step 2: On the top of the screen, select “Download PDF textbooks”
Step 3: From the “Classes” section, select your class.
Step 4: From “Medium”, select the medium suitable to you.
Step 5: All Maharashtra board books for your class will now be displayed on the right side.
Step 6: Click on the “Download” option to download the PDF book.

Who developed the Maharashtra State board books?

As of now, the MSCERT and Balbharti are responsible for the syllabus and textbooks of Classes 1 to 8, while Classes 9 and 10 are under the Maharashtra State Board of Secondary and Higher Secondary Education (MSBSHSE).

How many state boards are there in Maharashtra?

The Maharashtra State Board of Secondary & Higher Secondary Education, conducts the HSC and SSC Examinations in the state of Maharashtra through its nine Divisional Boards located at Pune, Mumbai, Aurangabad, Nasik, Kolhapur, Amravati, Latur, Nagpur and Ratnagiri.

About Maharashtra State Board (MSBSHSE)

The Maharashtra State Board of Secondary and Higher Secondary Education or MSBSHSE (Marathi: महाराष्ट्र राज्य माध्यमिक आणि उच्च माध्यमिक शिक्षण मंडळ), is an autonomous and statutory body established in 1965. The board was amended in the year 1977 under the provisions of the Maharashtra Act No. 41 of 1965.

The Maharashtra State Board of Secondary & Higher Secondary Education (MSBSHSE), Pune is an independent body of the Maharashtra Government. There are more than 1.4 million students that appear in the examination every year. The Maha State Board conducts the board examination twice a year. This board conducts the examination for SSC and HSC.

The Maharashtra government established the Maharashtra State Bureau of Textbook Production and Curriculum Research, also commonly referred to as Ebalbharati, in 1967 to take up the responsibility of providing quality textbooks to students from all classes studying under the Maharashtra State Board. MSBHSE prepares and updates the curriculum to provide holistic development for students. It is designed to tackle the difficulty in understanding the concepts with simple language with simple illustrations. Every year around 10 lakh students are enrolled in schools that are affiliated with the Maharashtra State Board.