Class 7: Maths Chapter 19 solutions. Complete Class 7 Maths Chapter 19 Notes.
Contents
Selina Class 7 ICSE Solutions Mathematics : Chapter 19- Congruency: Congruent Triangles
Selina 7th Maths Chapter 19, Class 7 Maths Chapter 19 solutions
Exercise 19 page: 213
1. State, whether the pairs of triangles given in the following figures are congruent or not:
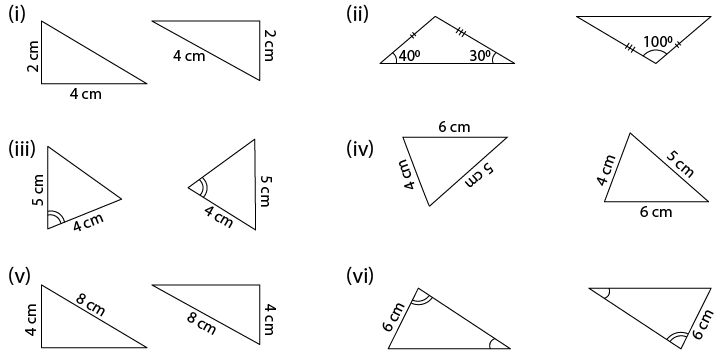
(vii) ∆ABC in which AB = 2 cm, BC = 3.5 cm and ∠C = 800 and, ∆DEF in which DE = 2cm, DF = 3.5 cm and ∠D = 800.
Solution:
(i) In the given figure, corresponding sides of the triangles are not equal.
Therefore, the given triangles are not congruent.
(ii) In the first triangle
Third angle = 1800 – (400 + 300)
By further calculation
= 1800 – 700
So we get
= 1100
In the two triangles, the sides and included angle of one are equal to the corresponding sides and included angle.
Therefore, the given triangles are congruent. (SAS axiom)
(iii) In the given figure, corresponding two sides are equal and the included angles are not equal.
Therefore, the given triangles are not congruent.
(iv) In the given figure, the corresponding three sides are equal.
Therefore, the given triangles are congruent. (SSS Axiom)
(v) In the right triangles, one side and diagonal of one triangle are equal to the corresponding side and diagonal of the other.
Therefore, the given triangles are congruent. (RHS Axiom)
(vi) In the given figure, two sides and one angle of one triangle are equal to the corresponding sides and one angle of the other.
Therefore, the given triangles are congruent. (SSA Axiom)
(vii) In ∆ ABC,
It is given that
AB = 2cm, BC = 3.5 cm, ∠C = 800
In ∆ DEF,
It is given that
DE = 2 cm, DF = 3.5 cm and ∠D = 800
We get to know that two corresponding sides are equal but the included angles are not equal.
Therefore, the triangles are not congruent.
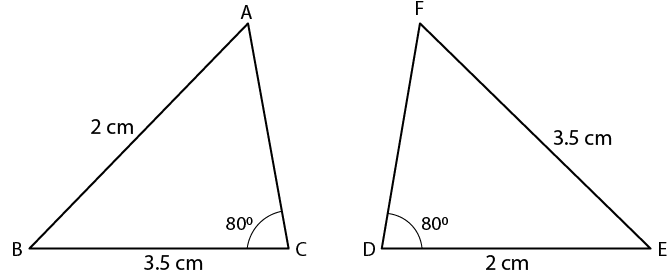
2. In the given figure, prove that:
∆ ABD ≅ ∆ ACD
Solution:
In ∆ ABD and ∆ ACD
AD = AD is common
It is given that
AB = AC and BD = DC
Here ∆ ABD ≅ ∆ ACD (SSS Axiom)
Therefore, it is proved.
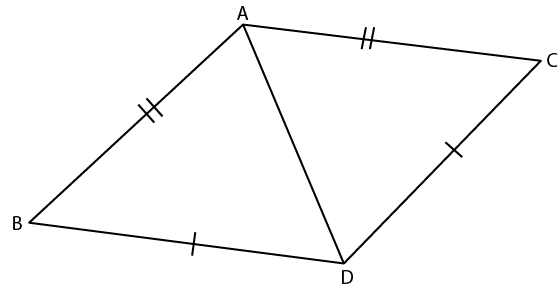
3. Prove that:
(i) ∆ ABC ≅ ∆ ADC
(ii) ∠B = ∠D
(iii) AC bisects angle DCB.
Solution:
In the figure
AB = AD and CB = CD
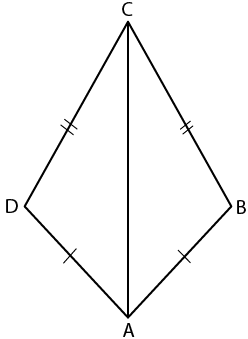
In ∆ ABC and ∆ ADC
AC = AC is common
It is given that
AB = AD and CB = CD
Here ∆ ABC ≅ ∆ ADC (SSS Axiom)
∠B = ∠D (c. p. c. t)
So we get
∠BCA = ∠DCA
Therefore, AC bisects ∠DCB.
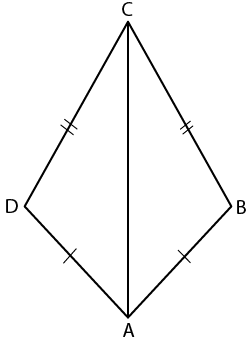
4. Prove that:
(i) ∆ABD ≡ ∆ACD
(ii) ∠B = ∠C
(iii) ∠ADB = ∠ADC
(iv) ∠ADB = 90°
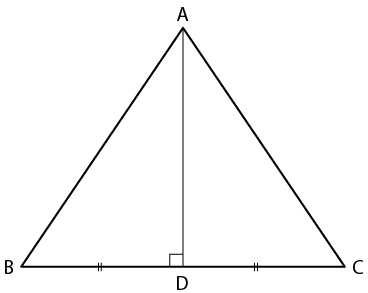
Solution:
From the figure
AD = AC and BD = CD
In ∆ABD and ∆ACD
AD = AD is common
(i) ∆ABD ≡ ∆ACD (SSS Axiom)
(ii) ∠B = ∠C (c. p. c. t)
(iii) ∠ADB = ∠ADC (c. p. c. t)
(iv) We know that
∠ADB + ∠ADC = 1800 is a linear pair
Here ∠ADB = ∠ADC
So we get
∠ADB = 1800/2
∠ADB = 90°
5. In the given figure, prove that:
(i) ∆ ACB ≅ ∆ ECD
(ii) AB = ED
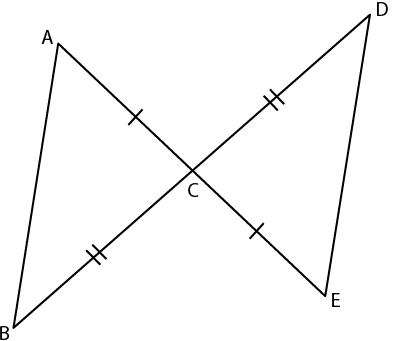
Solution:
(i) In ∆ ACB and ∆ ECD
It is given that AC = CE and BC = CD
∠ACB = ∠DCE are vertically opposite angles
Hence, ∆ ACB ≅ ∆ ECD (SAS Axiom)
(ii) Here AB = ED (c. p. c. t)
Therefore, it is proved.
6. Prove that
(i) ∆ ABC ≅ ∆ ADC
(ii) ∠B = ∠D
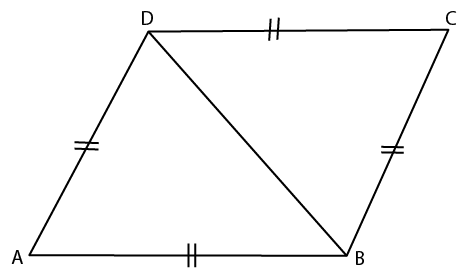
Solution:
(i) In ∆ ABC and ∆ ADC
It is given that
AB = DC and BC = AD
AC = AC is common
Hence, ∆ ABC ≅ ∆ ADC (SSS Axiom)
(ii) Here ∠B = ∠D (c. p. c. t)
Therefore, it is proved.
7. In the given figure, prove that:
BD = BC.
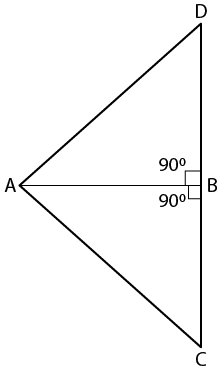
Solution:
In right ∆ ABD and ∆ ABC
AB = AB is common
It is given that
AD = AC
Hence, ∆ ABD ≅ ∆ ABC (RHS Axiom)
Here BD = BC (c. p. c. t)
Therefore, it is proved.
8. In the given figure, ∠1 = ∠2 and AB = AC.
Prove that:
(i) ∠B = ∠ C
(ii) BD = DC
(iii) AD is perpendicular to BC.
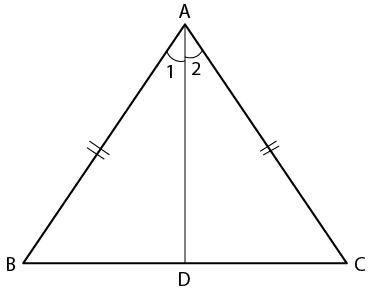
Solution:
In ∆ ADB and ∆ ADC
It is given that
AB = AC and ∠1 = ∠2
AD = AD is common
Hence, ∆ ADB ≅ ∆ ADC (SAS Axiom)
(i) ∠B = ∠C (c. p. c. t)
(ii) BD = DC (c. p. c. t)
(iii) ∠ADB = ∠ADC (c. p. c. t)
We know that
∠ADB + ∠ADC = 1800 is a linear pair
So we get
∠ADB = ∠ADC = 900
Here, AD is perpendicular to BC
Therefore, it is proved.
9. In the given figure, prove that:
(i) PQ = RS
(ii) PS = QR
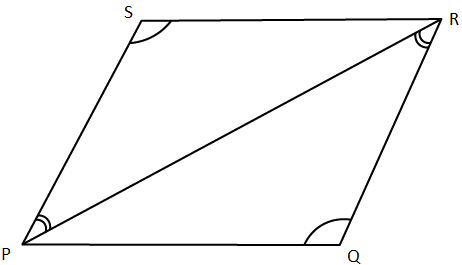
Solution:
In ∆ PQR and ∆ PSR
PR = PR is common
It is given that
∠PRQ = ∠RPS and ∠PQR = ∠PSR
∆ PQR ≅ ∆ PSR (AAS Axiom)
(i) PQ = RS (c. p. c. t)
(ii) QR = PS or PS = QR (c. p. c. t)
Therefore, it is proved.
10. In the given figure, prove that:
(i) ∆ XYZ ≅ ∆ XPZ
(ii) YZ = PZ
(iii) ∠YXZ = ∠PXZ
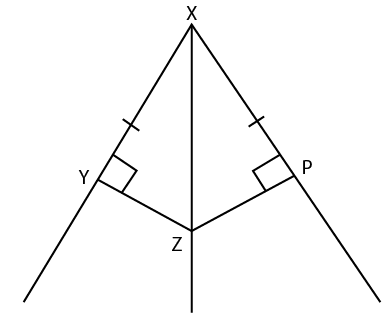
Solution:
In ∆ XYZ and ∆ XPZ
It is given that
XY = XP
XZ = XZ is common
(i) ∆ XYZ ≅ ∆ XPZ (RHS Axiom)
(ii) YZ = PZ (c. p. c. t)
(iii) ∠YXZ = ∠PXZ (c. p. c. t)
Therefore, it is proved.
11. In the given figure, prove that:
(i) ∆ ABC ≅ ∆ DCB
(ii) AC = DB
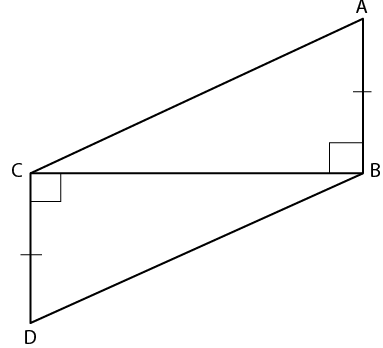
Solution:
In ∆ ABC and ∆ DCB
CB = CB is common
∠ABC = ∠BCD = 900
It is given that
AB = CD
(i) ∆ ABC ≅ ∆ DCB (SAS Axiom)
(ii) AC = DB (c. p. c. t)
Therefore, it is proved.
12. In the given figure, prove that:
(i) ∆ AOD ≅ ∆ BOC
(ii) AD = BC
(iii) ∠ADB = ∠ACB
(iv) ∆ADB ≅ ∆BCA
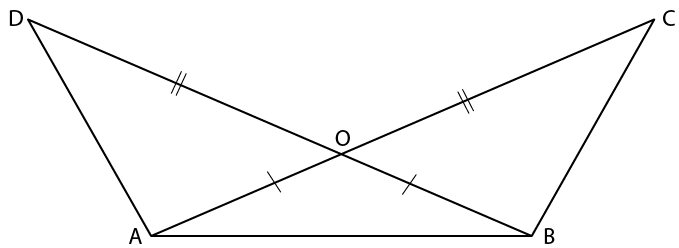
Solution:
In ∆ AOD and ∆ BOC
It is given that
OA = OB and OD = OC
∠AOD = ∠BOC are vertically opposite angles
(i) ∆ AOD ≅ ∆ BOC (SAS Axiom)
(ii) AD = BC (c. p. c. t)
(iii) ∠ADB = ∠ACB (c. p. c. t)
(iv) ∆ADB ≅ ∆BCA
It is given that
∆ADB = ∆BCA
AB = AB is common
Here ∆ AOB ≅ ∆ BCA
Therefore, it is proved.
13. ABC is an equilateral triangle, AD and BE are perpendiculars to BC and AC respectively. Prove that:
(i) AD = BE
(ii)BD = CE
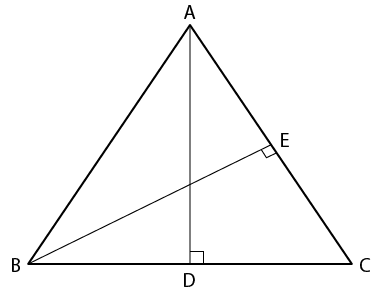
Solution:
In ∆ ABC
AB = BC = CA
We know that
AD is perpendicular to BC and BE is perpendicular to AC
In ∆ ADC and ∆ BEC
∠ADC = ∠BEC = 900
∠ACD = ∠BCE is common
AC = BC are the sides of an equilateral triangle
∆ ADC ≅ ∆ BEC (AAS Axiom)
(i) AD = BE (c. p. c. t)
(ii) BD = CE (c. p. c. t)
Therefore, it is proved.
14. Use the informations given in the following figure to prove triangles ABD and CBD are congruent.
Also, find the values of x and y.
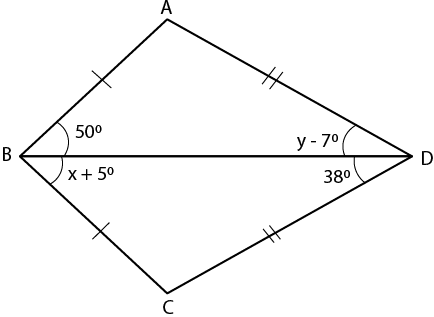
Solution:
In the figure
AB = BC and AD = DC
∠ABD = 500, ∠ADB = y – 70
∠CBD = x + 50, ∠CDB = 380
In ∆ ABD and ∆ CBD
BD = BD is common
It is given that
AB = BC and AD = CD
Here ∆ ABD ≅ ∆ CBD (SSS Axiom)
∠ABD = ∠CBD
So we get
50 = x + 5
x = 50 – 5 = 450
∠ADB = ∠CDB
y – 7 = 38
y = 38 + 7 = 450
Therefore, x = 450 and y = 450.
15. The given figure shows a triangle ABC in which AD is perpendicular to side BC and BD = CD. Prove that:
(i) ∆ ABD ≅ ∆ ACD
(ii) AB = AC
(iii) ∠B = ∠C
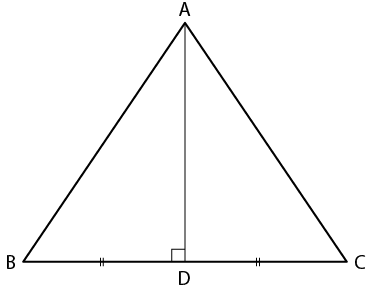
Solution:
(i) In ∆ ABC
AD is perpendicular to BC
BD = CD
In ∆ ABD and ∆ ACD
AD = AD is common
∠ADB = ∠ADC = 900
It is given that
BD = CD
∆ ABD ≅ ∆ CAD (SAS Axiom)
(ii) AB = AC (c. p. c. t)
(iii) ∠B = ∠C as ∆ ADB ≅ ∆ ADC
Therefore, it is proved.
Download PDF
Selina Class 7 ICSE Solutions Mathematics : Chapter 19- Congruency: Congruent Triangles
Chapterwise Selina Publishers ICSE Solutions for Class 7 Mathematics :
- Chapter 1- Integers
- Chapter 2- Rational Numbers
- Chapter 3- Fraction (Including Problems)
- Chapter 4- Decimal Fractions (Decimals)
- Chapter 5- Exponents (Including Laws of Exponents)
- Chapter 6- Ratio and Proportion (Including Sharing in a Ratio)
- Chapter 7- Unitary Method (Including Time and Work)
- Chapter 8- Percent and Percentage
- Chapter 9- Profit, Loss and Discount
- Chapter 10- Simple Interest
- Chapter 11- Fundamental Concepts (Including Fundamental Operations)
- Chapter 12- Simple Linear Equations (Including Word Problems)
- Chapter 13- Set Concepts
- Chapter 14- Lines and Angles (Including Construction of Angles)
- Chapter 15- Triangles
- Chapter 16- Pythagoras Theorem
- Chapter 17- Symmetry (Including Reflection and Rotation)
- Chapter 18- Recognition of Solids (Representing 3-D in 2-D)
- Chapter 19- Congruency: Congruent Triangles
- Chapter 20- Mensuration (Perimeter and Area of Plane Figures)
- Chapter 21- Data Handling
- Chapter 22- Probability
About Selina Publishers ICSE
Selina Publishers has been serving the students since 1976 and is one of the quality ICSE school textbooks publication houses. Mathematics and Science books for classes 6-10 form the core of our business, apart from certain English and Hindi literature as well as a few primary books. All these books are based upon the syllabus published by the Council for the I.C.S.E. Examinations, New Delhi. The textbooks are composed by a panel of subject experts and vetted by teachers practising in ICSE schools all over the country. Continuous efforts are made in complying with the standards and ensuring lucidity and clarity in content, which makes them stand tall in the industry.
